| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- TIMEOFWEEK
- 초분광이미지의분류
- ㅜ
- 용어정리 #GPS오차원인 #구조적원인 #기하학적오차 #SA
- GPSTIME
- 제7차국가공간정보정책
- Hyperspectral
- 경중률
- 사진의특수3점 #투영방법
- 측량및지형공간정보기술사 #출제기준 #출제유형
- 항공사진특수3점
- 국제원자시의정의
- 가우스곡선 #오차곡선 #확률밀도함수
- 수치표면모형
- 측량및지형공간기술사
- 초분광이미지
- Tasseled Cap 변환
- 기출문제 #기출문제분석 #반복출제 #측량및지형공간기술사
- Tasseled Cap
- 국제원자시의측정방법
- 경중률 #최확값
- 측량및지형공간기술사 #기출문제 #논술문제
- 제125회
- 국제원자시의원점
- 초분광영상처리요소기술
- 온맵 #국토지리정보원 #온맵제작
- 수치표고모형
- 비전 #목표 #추진전략
- GPSWEEK
- 수치표고자료
- Today
- Total
클라우드의 데일리 리포트
에피폴라 기하(Epipolar Geometry) 본문
1. 에피폴라 기하(Epipolar Geometry)
에피폴라 기하(Epipolar geometry)는 스테레오 비전(Stereo vision)과 관련된 개념으로, 두 개의 카메라로부터 얻은 영상 데이터를 이용하여 3D 공간에서의 점들을 추정하는 기법입니다.
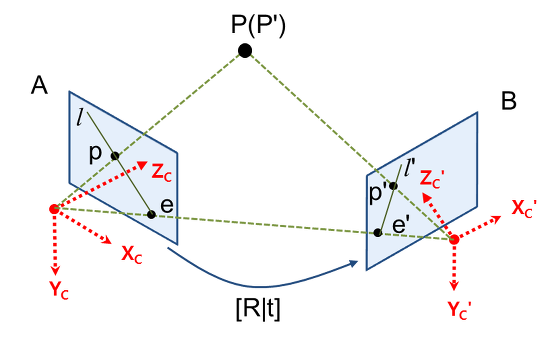
P(P'): 이미지 상에 맺힐 3차원 공간상의 점
p,p': 각 영상에서의 매칭 쌍
C,C': C는 왼쪽 카메라의 사영 원점(Center of Projection)이며, C'는 오른쪽 카메라의 사영 원점이다
e,e': 반대 영상의 카메라 센터가 행당 영상의 이미지에 맺힌 점을 EPIPOLE이라 부른다.
l,l': 각 영상에서 EPIPOLE(e,e')과 이미지 상의 점 (p,p')을 이은선을 EPILINE이라 부른다.
P(P'),C,C': 세점을 연결한 평면을 EPIPOLAR PLANE이라고 한다.
① 에피폴라 (Epipolar):
에피폴라는 스테레오 카메라 시스템에서 이미지 평면을 연결하는 직선으로, 다른 이미지에서 해당 점을 투영하는 교차점입니다. 에피폴라는 각 이미지에 대해 고정되어 있으며, 카메라의 위치와 방향에 의해 결정됩니다.
② 에피폴라 제약(Epipolar Constraint):
에피폴라 제약은 에피폴라 기하에서 중요한 개념으로, 한 이미지에서 특정 점의 대응점은 다른 이미지에서 해당 점의 에피폴라 상에 존재해야 함을 의미합니다. 이 제약은 이미지 간의 대응 관계를 제한함으로써 스테레오 매칭 문제를 해결하는 데 도움을 줍니다.
③ 에피폴라 평면(Epipolar Plane):
에피폴라 평면은 에피폴라와 이미지 평면을 포함하는 평면입니다. 스테레오 카메라 시스템에서 한 이미지의 특정 점을 다른 이미지로 투영할 때, 해당 점의 에피폴라는 에피폴라 평면 상에 존재합니다. 에피폴라 평면은 에피폴라 제약을 사용하여 대응 관계를 제한하는 데 사용됩니다.
2. 에피폴라 기하의 특징
에피폴라 기하는 스테레오 비전에서 매우 중요한 역할을 합니다. 두 개의 이미지로부터 대응되는 점들을 찾아내는 스테레오 매칭 문제를 해결하는 데 사용됩니다. 에피폴라 기하를 기반으로 한 알고리즘들은 에피폴라 제약을 활용하여 대응 점들을 찾고, 3차원 공간에서의 깊이 정보를 추정하는 데 활용됩니다.
1) 에피폴라 기하의 장점
정확한 3D 재구성: 에피폴라 기하를 사용하여 이미지 간의 대응 관계를 제약하는 것은 3D 재구성에 도움이 됩니다. 이를 통해 정확한 깊이 정보를 추정하고 객체의 형태와 위치를 파악할 수 있습니다.
깊이 정보의 밀도: 에피폴라 기하를 사용하면 각 이미지 픽셀에 대한 대응 픽셀을 찾을 수 있습니다. 이로 인해 깊이 정보의 밀도가 높아지며, 객체의 세부 사항과 윤곽을 더욱 정확하게 파악할 수 있습니다.
실시간 응용 가능: 에피폴라 기하를 사용한 스테레오 비전은 상대적으로 간단한 계산만 필요로 하기 때문에 실시간 응용에 적합합니다. 실시간 깊이 추정, 객체 추적 등의 응용에 활용할 수 있습니다.
2) 에피폴라 기하의 단점
계산 복잡성: 에피폴라 기하는 일반적으로 계산적으로 복잡한 작업입니다. 에피폴라 선을 찾는 데에는 이미지 매칭, 삼각화 및 행렬 연산과 같은 계산이 필요합니다. 큰 이미지나 복잡한 시스템에서는 계산 속도가 느려질 수 있습니다.
외부 제약 조건: 에피폴라 기하는 카메라 간의 상대적인 위치와 자세에 대한 제약 조건을 필요로 합니다. 카메라의 내부 파라미터와 외부 파라미터, 즉 카메라의 위치 및 방향에 대한 정확한 정보가 필요합니다. 이러한 외부 제약 조건을 얻기 위해 보정(calibration) 작업이 필요하며, 제약 조건이 부정확하거나 오차가 있는 경우 추정된 결과의 정확도를 저하시킬 수 있습니다.
픽셀 대응의 어려움: 에피폴라 기하는 일반적으로 텍스처가 있는 영역이나 잘 구분되는 특징점에서 가장 잘 작동합니다. 하지만 텍스처가 부족하거나 일부 영역에서는 특징점을 찾기 어렵거나 잘못된 특징점을 찾을 수 있습니다. 텍스처 없는 영역이나 반사나 투명한 재질 등의 경우에는 대응 픽셀을 정확하게 찾기 어려울 수 있습니다. 또한 이상한 점(Outliers)이 있는 경우 추정 결과에 큰 영향을 줄 수 있습니다.
