| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 경중률 #최확값
- 초분광이미지의분류
- ㅜ
- 제7차국가공간정보정책
- GPSWEEK
- 수치표고자료
- 사진의특수3점 #투영방법
- 제125회
- 수치표고모형
- Hyperspectral
- 온맵 #국토지리정보원 #온맵제작
- Tasseled Cap
- 측량및지형공간기술사 #기출문제 #논술문제
- 항공사진특수3점
- 경중률
- 국제원자시의정의
- 가우스곡선 #오차곡선 #확률밀도함수
- Tasseled Cap 변환
- 기출문제 #기출문제분석 #반복출제 #측량및지형공간기술사
- 초분광영상처리요소기술
- 국제원자시의측정방법
- 수치표면모형
- 측량및지형공간정보기술사 #출제기준 #출제유형
- 국제원자시의원점
- TIMEOFWEEK
- GPSTIME
- 용어정리 #GPS오차원인 #구조적원인 #기하학적오차 #SA
- 비전 #목표 #추진전략
- 초분광이미지
- 측량및지형공간기술사
- Today
- Total
클라우드의 데일리 리포트
위성의 궤도 요소 본문
1. 위성의 궤도 요소(케플러 요소)
궤도 요소(Orbital elements)는 특정한 궤도를 식별하기 위해 필요한 변수를 말한다. 보통 궤도는 케플러 요소라고 하는 6개의 요소로 정의되며, 섭동이 없는 궤도에서는 5개가 항상 일정하게 유지된다. 궤도를 도는 물체의 위치와 속도는 언제나 궤도 요소들에서 쉽게 추정할 수 있다.

케플러 6요소의 정의는 다음과 같다.
1) 궤도이심률(e)
타원의 형태, 즉 타원이 정확한 원으로부터 얼마나 어긋나있는지를 설명한다.

케플러 궤도의 이심률은 다음 4가지의 형태로 나타난다.
- 원 궤도:
- 타원 궤도:
- 포물선 궤도:
- 쌍곡선 궤도:
2) 궤도장반경(a)
- 궤도 근일점과 원일점의 평균값이다. 원 궤도의 경우에는 질량 중심과 물체의 거리가 아닌, 두 물체 사이의 거리를 나타낸다. 포물선이나 쌍곡선의 경우에는 이 값이 무한대로 나타난다.
- 행성의 궤도는 타원이기 때문에 반지름이 아닌 장반경과 단반경으로 정의한다. 장반경은 궤도 상에서 궤도 중심과 가장 거리가 먼 한 지점을 의미하며, 단반경은 궤도 상에서 궤도 중심과 가장 거리가 가까운 한 지점을 의미한다. 원일점, 근일점과의 차이는 측정의 기준이 되는 점이 항성이 아닌 궤도의 중심이라는 것이다. 포물선 궤도나 쌍곡선 궤도는 장반경이 무한대 이므로 단반경만을 가지게 된다.

3) 궤도 경사(i)
- 기준면에 대한 타원의 기울어진 정도를 말하고, 승교점(궤도가 기준면을 아래에서 위 방향으로 지나가는 점)에서의 궤도면과 기준면 사이의 각도로 측정되머, 그림에는 녹색 각도 i로 표시되어 있다.
4) 승교점 경도(Ω)
- 승교점은 궤도가 기준면 아래에서 위로 지나가는 지점을 가리키며, 기준점에서 반시계 방향으로 승교점까지 측정한 각도를 승교점 경도라 한다.
5) 근일점 편각(ω)
- 승교점으로부터 궤도 근일점(물체가 궤도를 돌 때 중심체와 가장 가까워지는 지점)까지의 각도로, 궤도면에서의 타원의 방향을 결정한다(그림에는 파란색 각도 ω로 표시되어 있다).
6) 진근점 이각(ν, θ, 또는 f)
- 행성이 궤도의 근일점을 통과한 시각에서의 물체의 위치를 결정한다. 평균근점이각(Mean Anomaly)은 시간에 따라 연속적으로 변화하는 "각도"로서 수학적으로 편리하지만, 각도가 기하학적인 각도와 일치하지 않는다. 이 값은 진근점이각(True anomaly) ν으로도 쓸 수 있는데, 이 값은 어느 시점에서나 궤도 근일점과 궤도를 도는 물체가 이루는 각도를 나타내어 각도가 기하학적인 각도와 일치한다.
평균 근점 이각 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 타원 궤도에서 단위시간당 지나간 면적(회색)과 가상의 원 궤도를 돌고 있는 천체(적색)의 공전 주기는 서로 같고, 따라서 같은 지역을 같은 시간 동안 지나간
ko.wikipedia.org
위 그림에서 실제 물체의 궤도는 회색 궤도이나, 저 궤도를 원이라고 가정한 빨간 궤도에서의 각거리를 구하는 것이다. 두 궤도의 공전 주기는 같기 때문에 같은 지역을 같은 시간 동안 지나간다. 근데 그림을 보면 원 궤도는 각 호들의 넓이가 일정하지만 타원 궤도인 회색 궤도는 일정하지 않다. 타원 궤도를 도는 물체는 초점과의 거리에 따라 각속도가 변하기 때문이다. 그래서 좀 더 구하기 쉬운 평균근점이각을 먼저 구한 후 타원 궤도에 이를 적용하게 된다.
평균근점이각을 구했으니 편심이각(Eccentric anomaly)를 구해야 한다. 편심이각은 그림으로 보는 게 더 직관적으로 이해하기가 쉽다.
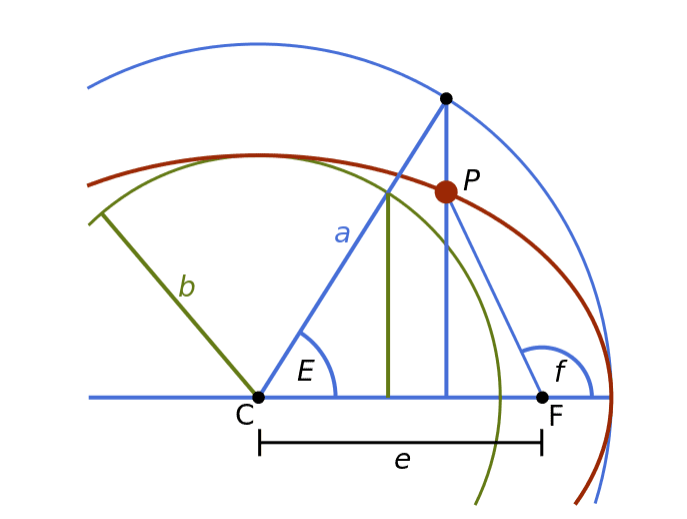
이 그림에서 물체의 위치를 P로 그에 따른 편심이각은 E로 나타내어지고 있다. 타원의 중심은 C이고 타원의 초점은 F이다. 이때 편심이각 E는 타원의 중심에 꼭지점 하나를 찍고 궤도 장반경과 같은 길이의 빗변 a를 그은 후, 장반경 e와 수직하면서도 P에 닿도록 선분을 그어 만들어진 직각삼각형에서 관찰되는 각이다.
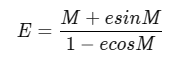
이 값들이 있다면 근일점 쪽을 X축으로 하는 황도좌표평면에 대한 직각 좌표 값을 계산할 수 있다. 그리고 이 좌표값의 유클리드거리 r과 진근점이각 v를 구할 수 있다. 진근점이각은 항성과 궤도의 근일점 기준으로 어느 각도에 행성이 위치하고 있는지를 나타내는 각이다. 즉, 행성은 항성으로부터 r만큼의 거리만큼 떨어져 있고 궤도의 근일점으로부터 v만큼 돌아간 위치에 존재하고 있다는 것이다.
