| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 초분광영상처리요소기술
- 비전 #목표 #추진전략
- 국제원자시의정의
- 용어정리 #GPS오차원인 #구조적원인 #기하학적오차 #SA
- 경중률 #최확값
- 사진의특수3점 #투영방법
- 측량및지형공간기술사 #기출문제 #논술문제
- TIMEOFWEEK
- 경중률
- 제7차국가공간정보정책
- GPSTIME
- ㅜ
- 초분광이미지의분류
- 제125회
- Tasseled Cap
- 국제원자시의원점
- 수치표고자료
- 항공사진특수3점
- 수치표면모형
- 측량및지형공간기술사
- 초분광이미지
- 국제원자시의측정방법
- 기출문제 #기출문제분석 #반복출제 #측량및지형공간기술사
- Tasseled Cap 변환
- GPSWEEK
- 가우스곡선 #오차곡선 #확률밀도함수
- 수치표고모형
- 측량및지형공간정보기술사 #출제기준 #출제유형
- 온맵 #국토지리정보원 #온맵제작
- Hyperspectral
- Today
- Total
클라우드의 데일리 리포트
불규칙 삼각망(TIN, Triangulated Irregular Network) 본문
1. 지형기복의 표현
지도상에 표현되는 공간객체는 3차원 현실세계의 자표(Earth Surface)상에 위치한다. 이러한 표면은 Z값을 갖는 한정된 수의 점으로 이루어진 연속적 분포면으로 표현될 수 있고, 표현되는 방식에 의해 정규형태의 표면, 비정규형태의 표면으로 구분하다. 지형 기복은 지형의 고도 변화나 경사를 나타내는 것으로, 지형 데이터를 시각적으로 표현할 때 매우 중요한 역할을 합니다. 지형 기복을 표현하는 방법에는 다음과 같은 것들이 있다.
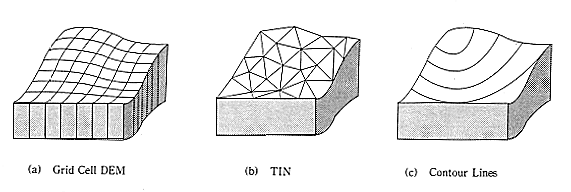
1) DEM(Digital Elevation Model)
지형표면의 높이를 일정 간격으로 측정하여 만든 수치표고모델로 공간정보(지도 및 항공사진, 위성영상 등)를 입체화할 수 있다. 수치표고모델(DEM:Digital Elevaiton Model)과 같은 정규표면은 Z값을 갖는 동일한 크기의 정규격자로 구성된다.
2) TIN(Triangulated Irregular Network)
지형을 삼각형으로 나누어 구성하는 방법이다. 각 삼각형의 변화에 따라 지형의 기복을 시각적으로 표현할 수 있다.
3) 등고선 (Contour Lines)
지형의 높이를 나타내는 등고선은 가장 일반적인 지형 기복 표현 방법 중 하나이다. 등고선은 지형의 고저차이를 시각적으로 표현하는 데 적합하며, 일반적으로 고도가 같은 점을 연결하여 등고선을 그린다.
2. TIN(Triangulated Irregular Network)
1) TIN 정의
딜로니 삼각분할(DelaunayTriangulation)은 대부분의 삼각형들이 거의 균일한 각을 갖는 일반적인 성질 때문에 근사화(approximation)를 위해 주로 사용되는 방법이다. 딜로니 삼각분할은 주어진 임의의 정점 집합 P에 대해 유일한 삼각 분할을 생성하여 준다. 그리고 이 삼각분할 수행 결과로 생긴 면들을 딜로니 삼각형(Delaunay triangles)이라 부른다. 지형기복을 표현하는데 중요한 지점을 델로니 삼각형(Delaunay triangulation)정의에 따라 불규칙 형태의 연속적인 삼각형으로 연결시킨 위상 자료구조를 TIN이라 한다.
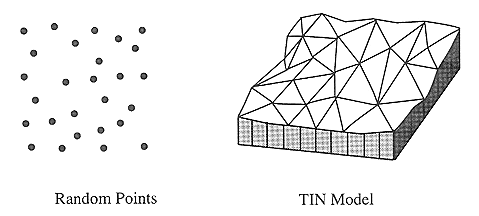
2) TIN 생성방법
딜로니 삼각분할은 평면위의 점들을 삼각형으로 연결하여 공간을 분할할 때, 이 삼각형들의 내각의 최소값이 최대가 되도록 하는 분할을 말한다. 딜로니 삼각형은 외접하는 원 내부에 삼각형의 꼭지점외에 다른 점이 없도록 연결시킨 삼각형이다. 표고 추출지점을 대상으로 티센 다각형을 만들고 표고 추출지점을 연결하는 삼각형의 변이 티센 다각형의 한 변을 이등분하는 형태로 델로니 삼각형을 연결해 나간다.
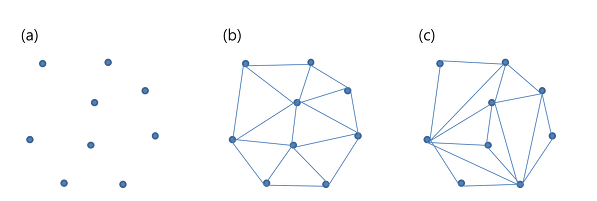
위 그림 (a)와 같이 점들이 있을 때 이 점들을 연결하여 삼각형을 만드는 방법은 (b), (c)와 같이 다양하다. 딜로니 삼각분할은 이러한 여러 삼각분할 중에서 (b)와 같이 각각의 삼각형들이 최대한 정삼각형에 가까운 즉, (c)와 같이 길쭉하고 홀쭉한 삼각형이 나오지 않도록 하는 분할을 말한다.
딜로니 삼각분할의 가장 중요한 특징중 하나는, "어떤 삼각형의 외접원도 그 삼각형의 세 꼭지점을 제외한 다른 어떤 점도 포함하지 않는다" 이다. (이를 empty circumcircle property라고 부른다). 삼각형이 홀쭉하고 길수록 외접원도 커짐을 생각하면 된다. 위 그림에서 (b)는 이 조건을 만족하고 (c)는 만족하지 않음을 쉽게 확인할 수 있다.
3) TIN 특징
TIN은 불규칙한 점, 선, 다각형 내에 각각의 중요한 정보를 포함하고 있기 때문에 지형의 기복이 심한 지역에서 보다 더 효과적으로 지형을 표현할 수 있어 규칙격자형 구조에 비해 자료의 중복을 줄일 수 있다. 즉, 기복의 변화가 적은 지역에서는 표고 추출지점의 간격을 늘려 추출지점의 수를 줄이고, 지형 기복변화가 심한 지역에서는 표고 추출지점의 수를 증가시킴으로써, 지형을 효과적으로 표현하면서도 자료의 전체적인 량을 줄일 수 있다. TIN모델은 3차원 공간에서 구분되어 연결된 선형모델이므로 연속 삼각형 형태로 쉽게 도해적으로 표시된다. 또한, 경사도 및 방향 등의 계산에 매우 효율적이다.
3. DEM vs TIN
DEM은 그리드 형태의 데이터를 사용하며, 일정한 해상도와 높은 수직 정확도를 가지고 있어 지형 분석에 적합합니다. 또한 작은 메모리 사용량과 빠른 구축 시간으로 인해 대규모 지형 데이터 처리에 적합합니다. 시각화에도 용이하며, 자연 지리학, 지형 공간 분석, 환경 모니터링 등의 분야에서 사용됩니다. 반면, TIN은 삼각형 형태의 데이터를 사용하며, 지형의 복잡성에 따라 해상도가 달라집니다. 지형 분석 및 3D 모델링, 시뮬레이션, 가시화, 엔지니어링 분야에서 사용됩니다. TIN은 구축 시간이 오래 걸리고, 메모리 사용량이 크기 때문에 작은 규모의 데이터 처리에 적합합니다. 또한, 기울기에 따라 정확도가 다를 수 있습니다.
| DEM | TIN | |
| 데이터유형 | Grid 형태 | Triangular 형태 |
| 데이터크기 | 큰 데이터 처리 용이 | 작은 데이터 처리 용이 |
| 데이터 해상도 | 일정한 해상도 | 지형의 복잡성에 따라 해상도가 다름 |
| 데이터 정확도 | 높은 수준의 수직 정확도 | 기울기에 따라 정확도가 다를 수 있음 |
| 메모리 사용량 | 작은 메모리 사용량 | 큰 메모리 사용량 |
| 데이터 구축 시간 | 구축 시간이 빠름 | 구축 시간이 오래 걸림 |
| 시각화 | 그라데이션, 쉐이딩, 경사도 시각화에 적합 | 불규칙 GRID 시각화에 적합 |
| 지형의 복잡성 | 지형의 복잡성이 낮은 경우에 적합 | 지형의 복잡성이 높은 경우에 적합 |
